[NOIP1999 普及组] Cantor 表

题目描述

现代数学的著名证明之一是 Georg Cantor 证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的：

$1/1$ , $1/2$ , $1/3$ , $1/4$, $1/5$, …

$2/1$, $2/2$ , $2/3$, $2/4$, …

$3/1$ , $3/2$, $3/3$, …

$4/1$, $4/2$, …

$5/1$, …

…

我们以 Z 字形给上表的每一项编号。第一项是 $1/1$，然后是 $1/2$，$2/1$，$3/1$，$2/2$，…

输入格式

整数$N$（$1 \leq N \leq 10^7$）。

输出格式

表中的第 $N$ 项。

样例 #1

样例输入 #1

7

样例输出 #1

1/4

题目中的z字型就是下图

1.观察斜线中的数字数量规律第一条斜线，就是1/1
第二条斜线，就是1/2,2/1
第三条斜线，就是3/1,2/2/,1/3

可以观察到是一个等差数列，根据等差数列求和公式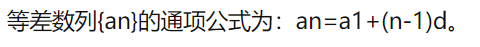
根据Sn>N这个公式，可以解出n,n是这一项在第几条斜线的位置

tips:N是题目中给的第N项

2.算出该项在该斜线中是第几项
Sn-Sn-1就是该项在该斜线中是第几项

3.奇数偶数行的分子分母规律观察即可

下面贴出代码

#include<stdlib.h>
#include<stdio.h>
int main(){
    int n;
    int row,row_num=0,row_pre_num,row_inline_index;
    scanf("%d",&n);
    int i=1;
    while (1)
    {   
        row_num=i+i*(i-1)*(1.0/2);
        if(row_num>=n){
            break;
        }
        i++;
    }
    row=i;
    row_pre_num=(row-1)+(row-1)*((row-1)-1)*(1.0/2);
    row_inline_index=n-row_pre_num-1;
    if(row%2==0){
        printf("%d/%d",1+row_inline_index,row-row_inline_index);
    }
    else{
        printf("%d/%d",row-row_inline_index,1+row_inline_index);
    }
    system("pause");
    return 0;
}